A close look at the VIX index shows a very skewed distribution as low levels push against a barrier. There is more risk that the VIX will rise versus fall. The same can be said for many other asset prices. Normality is out; non-normality with respect to distributions is in. The value of looking beyond standard deviation is all the more important in the current environment.
These distribution tilts are all the more important impact in any discussion of asset allocation, but does not change the fact that risk management is still about the downside of any distribution. The lower partial movements can capture the deviations from normality and is a generalization of semi-variance that was discussed in a previous post, “Measuring Risk – Working Against the Downside”. The semi-variance is just the lower partial second moment, so there should be little problem looking at the lower partial moment of higher degrees like skew, the third moment. There is simplicity with semi-variance as an extension of risk measurement of the standard deviation, but the work on lower and upper partial moments is not hard to implement in a spreadsheet.
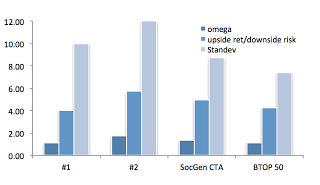
Why not just look at volatility? Because volatility is too restrictive in a more complex price and return world where normality is the exception. The cost of skew and fat tails are real for those who ignore them. A simple example is shown with two managed futures funds and two managed futures indices. We looked at the standard deviation for each over the last three years as well as the omega or upside versus downside returns and the upside return versus downside risk. The fund that has the highest standard deviation or risk also has the highest upside to downside capture and the highest upside return to downside risk. The “riskiest” fund has the best upside opportunity and this applies to different threshold levels beyond zero.
This work on partial moments can be extended to comparisons with the market portfolio. The covariance/variance (beta) of a stock to the market will be same as the conditional lower partial movement to lower partial moment of the market when the distribution is normal. If returns are not normal, there will be greater deviations between the normally calculated beta and partial moments beta based on the distance from the average market exposure. This means that your beta measure for alternative assets which may have low market betas will have greater measurement error when there is non-normality. Your measure of risk to the market will deviate from normal beta calculations as the partial moments start to deviate from normal.
Lower partial moments like semi-variance splits the distribution between good and bad volatility as measured by a target that in most cases is set to zero or the mean return, but investors can look beyond symmetric distributions. We have found that downside risk measures relative to a target return are especially useful for pensions. Their interest are whether returns will be below their expected return not the around the average return of the manager.
Don’t be fooled by standard deviation when a little extra effort can generate useful information on downside risk. “Risky” managers, based on standard deviation, may actually be winners as measured by downside risk or lower partial moments.